Note

This tutorial was generated from a Jupyter notebook that can be downloaded here.

Where’s the spot?

An example of how to solve for the location, amplitude, and size of a star spot.

As we discuss in this notebook, starry isn’t really meant for modeling discrete features such as star spots; rather, starry employs spherical harmonics to model the surface brightness distribution as a smooth, continuous function. We generally recommend approaching the mapping problem in this fashion; see the Eclipsing Binary tutorials for more information on how to do this. However, if you really want to model the surface of a star with star spots, read on!

Let’s begin by importing stuff as usual:

import numpy as np
import starry
import exoplanet as xo
import pymc3 as pm
import matplotlib.pyplot as plt
from corner import corner

starry.config.quiet = True

We discussed how to add star spots to a starry map in this tutorial. Here, we’ll generate a synthetic light curve from a star with a single large spot with the following parameters:

# True values
truth = dict(amp=-0.01, sigma=0.025, lat=30, lon=30)

Those are, respectively, the fractional amplitude of the spot, its standard deviation (recall that the spot is modeled as a Gaussian in \(\cos\Delta\theta\), its latitude and its longitude.

To make things simple, we’ll assume we know the inclination and period of the star exactly:

# Things we'll assume are known
inc = 60.0
P = 1.0

Let’s instantiate a 15th degree map and give it those properties:

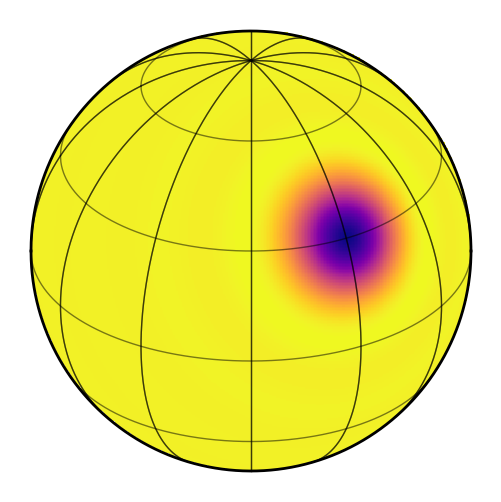
map = starry.Map(15)
map.inc = inc
map.add_spot(amp=truth["amp"], sigma=truth["sigma"], lat=truth["lat"], lon=truth["lon"])
map.show()

Now we’ll generate a synthetic light curve with some noise:

t = np.linspace(0, 3.0, 500)
flux0 = map.flux(theta=360.0 / P * t).eval()
np.random.seed(0)
flux_err = 2e-4
flux = flux0 + flux_err * np.random.randn(len(t))

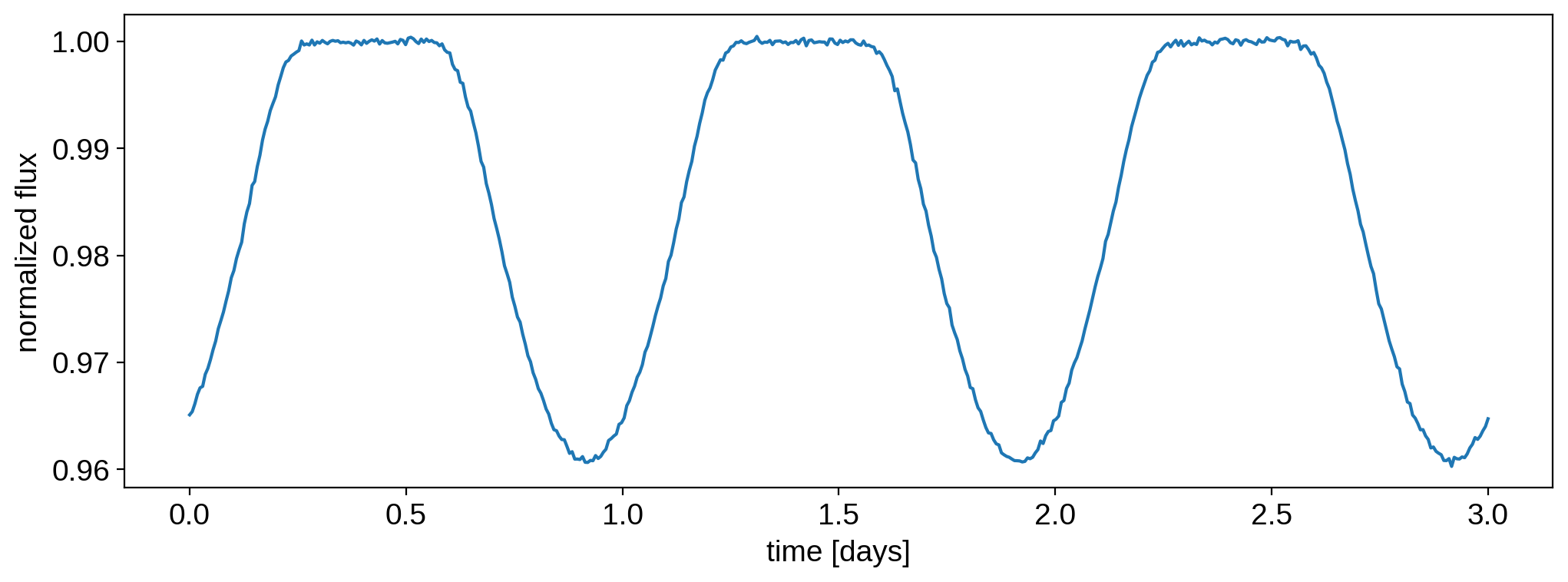
Here’s what that looks like:

plt.plot(t, flux)
plt.xlabel("time [days]")
plt.ylabel("normalized flux");

In this notebook, we are going to derive posterior constraints on the spot properties. Let’s define a pymc3 model and within it, our priors and flux model:

with pm.Model() as model:

    # Priors
    amp = pm.Uniform("amp", lower=-0.1, upper=0.0, testval=-0.02)
    sigma = pm.Uniform("sigma", lower=0.0, upper=0.1, testval=0.01)
    lat = pm.Uniform("lat", lower=-90.0, upper=90.0, testval=0.1)
    lon = pm.Uniform("lon", lower=-180.0, upper=180.0, testval=0.1)

    # Instantiate the map and add the spot
    map = starry.Map(ydeg=15)
    map.inc = inc
    map.add_spot(amp=amp, sigma=sigma, lat=lat, lon=lon)

    # Compute the flux model
    flux_model = map.flux(theta=360.0 / P * t)
    pm.Deterministic("flux_model", flux_model)

    # Save our initial guess
    flux_model_guess = xo.eval_in_model(flux_model)

    # The likelihood function assuming known Gaussian uncertainty
    pm.Normal("obs", mu=flux_model, sd=flux_err, observed=flux)

Note

It’s important to define a nonzero testval for both the latitude and longitude of the spot. If you don’t do that, it’s likely the optimizer will get stuck at lat, lon = 0, 0, which is a local maximum of the likelihood.

We’ve placed some generous uniform priors on the four quantities we’re solving for. Let’s run a quick gradient descent to get a good starting position for the sampler:

%%time
with model:
    map_soln = xo.optimize(start=model.test_point)

optimizing logp for variables: [lon, lat, sigma, amp]
125it [00:01, 88.00it/s, logp=3.544180e+03]

CPU times: user 2.74 s, sys: 410 ms, total: 3.15 s
Wall time: 14.6 s

message: Desired error not necessarily achieved due to precision loss.
logp: -2029337.317471879 -> 3544.179658502205

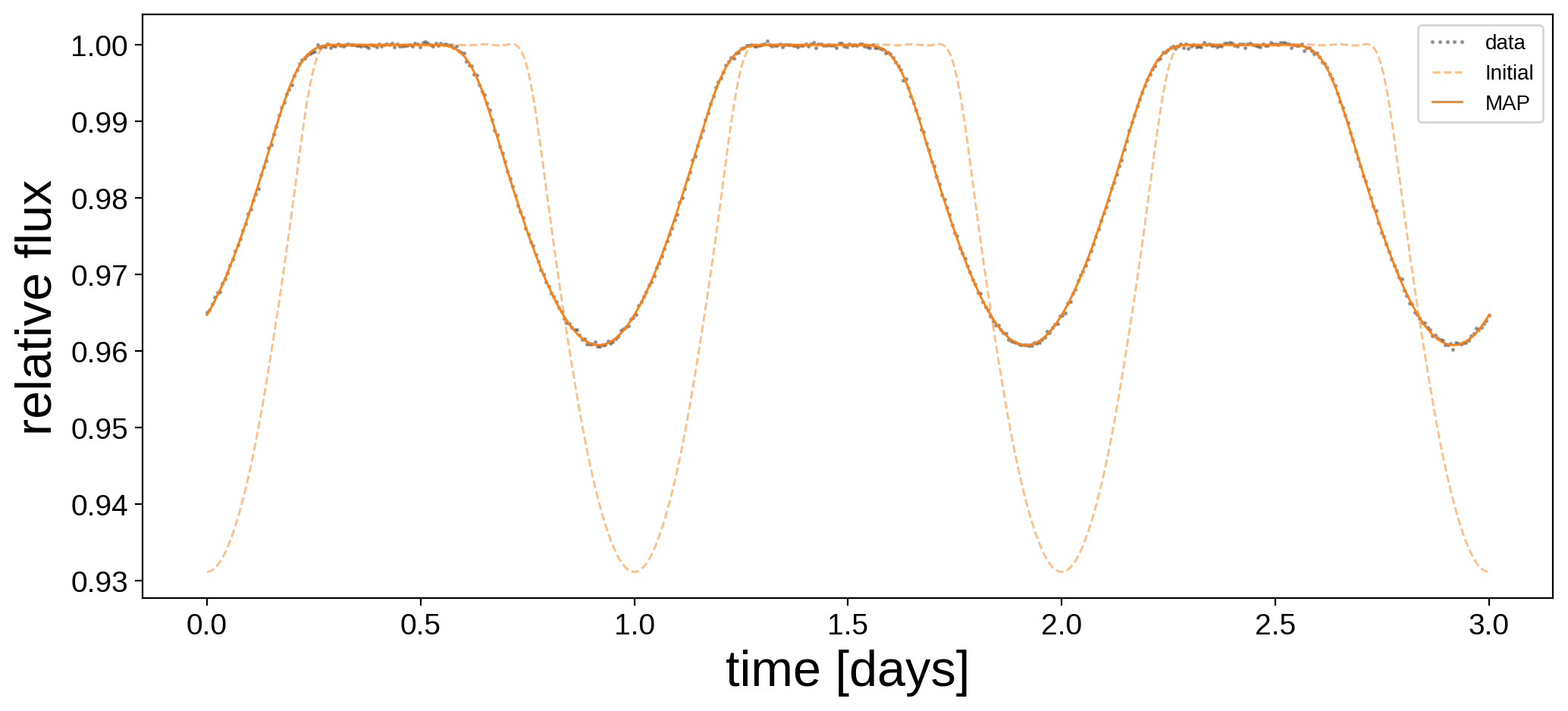
Here’s the data and our initial guess before and after the optimization:

plt.figure(figsize=(12, 5))
plt.plot(t, flux, "k.", alpha=0.3, ms=2, label="data")
plt.plot(t, flux_model_guess, "C1--", lw=1, alpha=0.5, label="Initial")
plt.plot(
    t, xo.eval_in_model(flux_model, map_soln, model=model), "C1-", label="MAP", lw=1
)
plt.legend(fontsize=10, numpoints=5)
plt.xlabel("time [days]", fontsize=24)
plt.ylabel("relative flux", fontsize=24);

And here are the maximum a posteriori (MAP) values next to the true values:

print("{0:12s} {1:10s} {2:10s}".format("", "truth", "map_soln"))
for key in truth.keys():
    print("{0:10s} {1:10.5f} {2:10.5f}".format(key, truth[key], map_soln[key]))

             truth      map_soln
amp          -0.01000   -0.01001
sigma         0.02500    0.02552
lat          30.00000   29.89098
lon          30.00000   29.96577

Not bad! Looks like we recovered the correct spot properties. But we’re not done! Let’s get posterior constraints on them by sampling with pymc3. Since this is such a simple problem, the following cell should run in about a minute:

%%time
with model:
    trace = pm.sample(
        tune=250,
        draws=500,
        start=map_soln,
        chains=4,
        step=xo.get_dense_nuts_step(target_accept=0.9),
    )

Sequential sampling (4 chains in 1 job)
NUTS: [lon, lat, sigma, amp]
Sampling chain 0, 0 divergences: 100%|██████████| 750/750 [00:32<00:00, 23.08it/s]
Sampling chain 1, 0 divergences: 100%|██████████| 750/750 [00:08<00:00, 83.34it/s]
Sampling chain 2, 0 divergences: 100%|██████████| 750/750 [00:09<00:00, 82.71it/s]
Sampling chain 3, 0 divergences: 100%|██████████| 750/750 [00:08<00:00, 83.69it/s]
The acceptance probability does not match the target. It is 0.9669577098407267, but should be close to 0.9. Try to increase the number of tuning steps.

CPU times: user 1min 8s, sys: 488 ms, total: 1min 8s
Wall time: 1min 13s

Plot some diagnostics to assess convergence:

var_names = ["amp", "sigma", "lat", "lon"]
display(pm.summary(trace, var_names=var_names))

	mean	sd	hpd_3%	hpd_97%	mcse_mean	mcse_sd	ess_mean	ess_sd	ess_bulk	ess_tail	r_hat
amp	-0.010	0.000	-0.010	-0.010	0.000	0.000	1903.0	1903.0	1902.0	1635.0	1.0
sigma	0.026	0.001	0.024	0.027	0.000	0.000	1971.0	1968.0	1975.0	1586.0	1.0
lat	29.890	0.096	29.717	30.070	0.002	0.001	2514.0	2514.0	2536.0	1743.0	1.0
lon	29.966	0.031	29.909	30.024	0.001	0.000	1958.0	1958.0	1958.0	1519.0	1.0

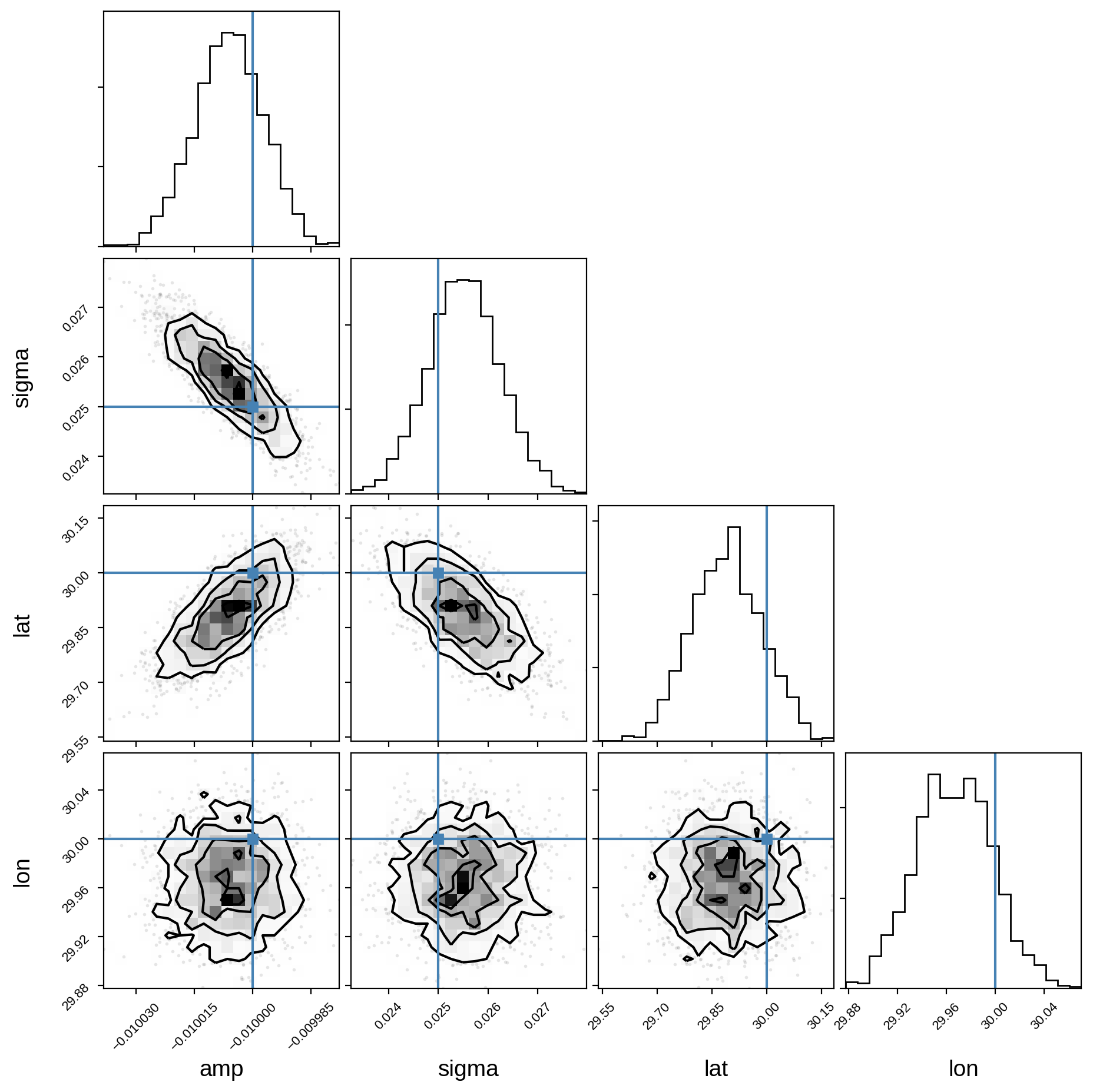
And finally, the corner plot showing the joint posteriors and the true values (in blue):

samples = pm.trace_to_dataframe(trace, varnames=var_names)
corner(samples, truths=[truth[name] for name in var_names]);

We’re done! It’s easy to extend this to multiple spots, simply by calling map.add_spot once for each spot in the model, making sure you define new pymc3 variables for the spot properties of each spot.